Με την επικείμενη πανωλεθρία των υποψηφίων στα Μαθηματικά των Επιστημών Οικονομίας και Πληροφορικής, όπως κάθε χρόνο, άρχισαν οι προτροπές προς το Υπουργείο Παιδείας να διαχωριστούν τα Μαθηματικά του 2ου Πεδίου από τα Μαθηματικά του 4ου Πεδίου.
Το επιχείρημα είναι ότι τα Μαθηματικά που χρειάζονται στα Οικονομικά δεν είναι τόσο πολλά όσα χρειάζονται στο Πολυτεχνείο. Σωστό είναι αυτό, αλλά στο 4ο Πεδίο υπάρχουν και οι σχολές Πληροφορικής, εκεί η μαθηματική σκέψη είναι παραπάνω από απαραίτητη. Τα διαφορετικά Μαθηματικά ίσχυαν και τον καιρό των δεσμών (1983-1999).
Ας δούμε τι συμβαίνει. Στον πίνακα βλέπουμε τις επιδόσεις στα Μαθηματικά σε κάθε Πεδίο. Η διαφορά είναι πολύ μεγάλη. Στο 2ο Πεδίο τα τρία τελευταία χρόνια το ποσοστό των υποψηφίων που έγραψε κάτω από το 10 ήταν από 27,58% έως 34,99%. Στο ίδιο διάστημα στο 4ο Πεδίο το ποσοστό ήταν από 70,04% έως 73,56%, δηλαδή υπερδιπλάσιο. Το ποσοστό των αριστούχων στα Μαθηματικά των υποψηφίων του 2ου Πεδίου ήταν πενταπλάσιο του αριθμού των αριστούχων του 4ου Πεδίου. Προφανώς όταν η αποτυχία είναι τόσο μεγάλη καταλαβαίνουμε ότι τα θέματα που τέθηκαν ήταν πάνω από το επίπεδο των υποψηφίων, συνεπώς ήταν ακατάλληλα γι’ αυτούς.
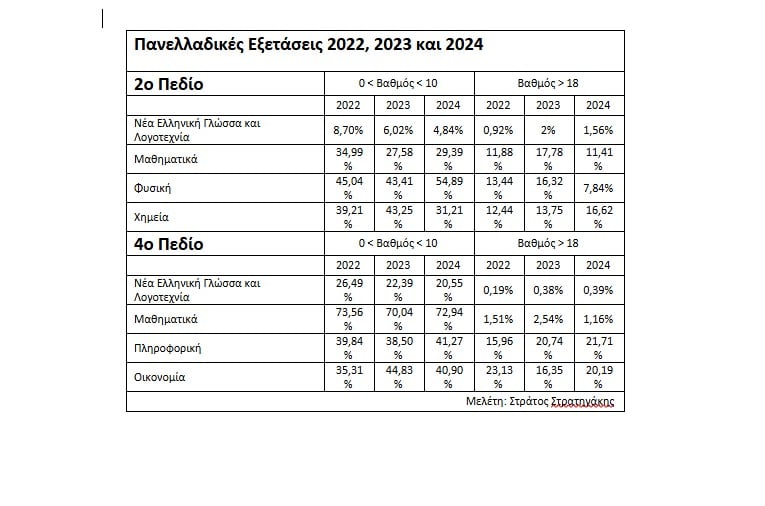
Αν δούμε και τις επιδόσεις στη Νέα Ελληνική Γλώσσα και Λογοτεχνία των υποψηφίων των δύο Πεδίων, το δεύτερο μάθημα στο οποίο τα θέματα είναι κοινά. Το ποσοστό των υποψηφίων του 2ου Πεδίου με βαθμολογία μικρότερη του 10 κυμάνθηκε από 4,84% έως 8,70%, ενώ στο 4ο Πεδίο το ποσοστό ήταν από 20,55% έως 26,49%. Παραπάνω από τριπλάσιος αριθμός υποψηφίων του 4ου Πεδίου έγραψε κάτω από 10 σε σχέση με τους υποψηφίους του 2ου Πεδίου. Αντίστοιχα οι αριστούχοι του 2ου Πεδίου ήταν περίπου πενταπλάσιοι από τον αριθμό των αριστούχων του 4ου Πεδίου.
Οι τόσο μεγάλες διαφορές και στη Γλώσσα και στα Μαθηματικά μας δείχνουν ότι υπάρχει διαφορά στο επίπεδο των υποψηφίων των δύο Πεδίων. Στα άλλα δύο μαθήματα κάθε Πεδίου, που δεν είναι κοινή η ύλη και τα θέματα (αφού είναι διαφορετικά μαθήματα) οι επιδόσεις είναι παραπλήσιες. Αυτό συμβαίνει διότι η Πληροφορική και η Οικονομία είναι ευκολότερες από τη Φυσική και τη Χημεία. Η Φυσική και η Χημεία απαιτούν από τους υποψηφίους υποδομή από τις προηγούμενες τάξεις, κάτι που δεν συμβαίνει με την Πληροφορική και την Οικονομία. Έτσι τα ευκολότερα μαθήματα ισοφαρίζουν το χαμηλότερο επίπεδο των υποψηφίων του 4ου Πεδίου και δημιουργούν παρόμοιες επιδόσεις.
Στο 2ο και το 4ο Πεδίο υπάρχουν 57 κοινά Τμήματα με 10.829 εισακτέους. Από αυτούς οι 9746 είναι από το Γενικό Λύκειο. Σ’ αυτά τα Τμήματα οι υποψήφιοι του 4ου Πεδίου διαγωνίζονται με τους υποψηφίους του 2ου Πεδίου. Το πλεονέκτημα που έχουν είναι πολύ μεγάλο, αφού διαπιστώσαμε ότι είναι χαμηλότερου επιπέδου (κατά μέσο όρο βέβαια) αλλά στα δύο από τα τέσσερα μαθήματα αυτό δεν φαίνεται, αφού οι επιδόσεις στην Πληροφορική και την Οικονομία είναι παρόμοιες με τη Φυσική και τη Χημεία. Σ’ αυτά τα κοινά Τμήματα θα προστεθούν από του χρόνου και οι Στρατιωτικές σχολές, αυξάνοντας τον αριθμό των κοινών σχολών.
Το πλεονέκτημα των υποψηφίων του 4ου Πεδίου έναντι των υποψηφίων του 2ου Πεδίου στις κοινές σχολές έχει γίνει αντιληπτό από τους υποψηφίους που τα τελευταία χρόνια επιλέγουν μαζικά το 4ο Πεδίο. Οι υποψήφιοι από το 4ο Πεδίο είναι πια διπλάσιοι από τους υποψηφίους του 2ου Πεδίου. Τι θα γίνει αν τα Μαθηματικά αποκτήσουν διαφορετική ύλη και θέματα για τους υποψηφίους; Οι υποψήφιοι από το 4ο Πεδίο θα έχουν ευκολότερα θέματα και, συνεπώς η σύγκριση των βαθμολογιών μεταξύ των υποψηφίων του 2ου και του 4ου Πεδίου θα είναι εντελώς άδικη για τους υποψηφίους του 2ου Πεδίου. Αυτό θα έχεε ως αποτέλεσμα ότι όλο και περισσότεροι υποψήφιοι θα στρέφονται προς το 4ο Πεδίο και οι σχολές του 2ου Πεδίου θα μείνουν χωρίς φοιτητές.
Το παράλογο που ισχύει σε όλες τις κοινές σχολές και είναι το μεγαλύτερο πρόβλημα του εξεταστικού μας συστήματος θα ενταθεί. Υποψήφιοι εξετάζονται σε διαφορετικά θέματα και μετά συγκρίνονται οι υποψήφιοι ως προς το ποιος έγραψε καλύτερα ενώ τα μαθήματα είναι διαφορετικά. Τώρα θα έχουμε το ίδιο μάθημα τα Μαθηματικά σε δύο εκδόσεις μία κανονική και μία light και θα συγκρίνονται οι βαθμοί των υποψηφίων στο κανονικό και το light για τις κοινές σχολές. Εντελώς παράλογο. Είναι σαν να επιδοτείς τους αδύνατους υποψηφίους για να φτάσουν τους καλούς. Αντί να λυθεί κάποιο πρόβλημα δημιουργούμε ακόμη ένα, που κάνει την κατάσταση ακόμα χειρότερη. Αν δεν υπήρχαν κοινές σχολές θα ήταν λογικό να είναι διαφορετικά τα Μαθηματικά. Αλλά με τόσες κοινές σχολές είναι παράλογο.
Όλα αυτά γίνονται διότι με συνεχή μπαλώματα επιχειρείται να βελτιωθεί ένα σύστημα που βρίσκεται ήδη αρκετές δεκαετίες πίσω. Η μόνη λύση είναι η δημιουργία ενός συστήματος πρόσβασης στα Πανεπιστήμια που εκτός από αδιάβλητο θα είναι και δίκαιο. Γίνεται; Φυσικά και γίνεται όταν υπάρχει θέληση, που δυστυχώς δεν υπάρχει.














